類神經網路 Neural Network

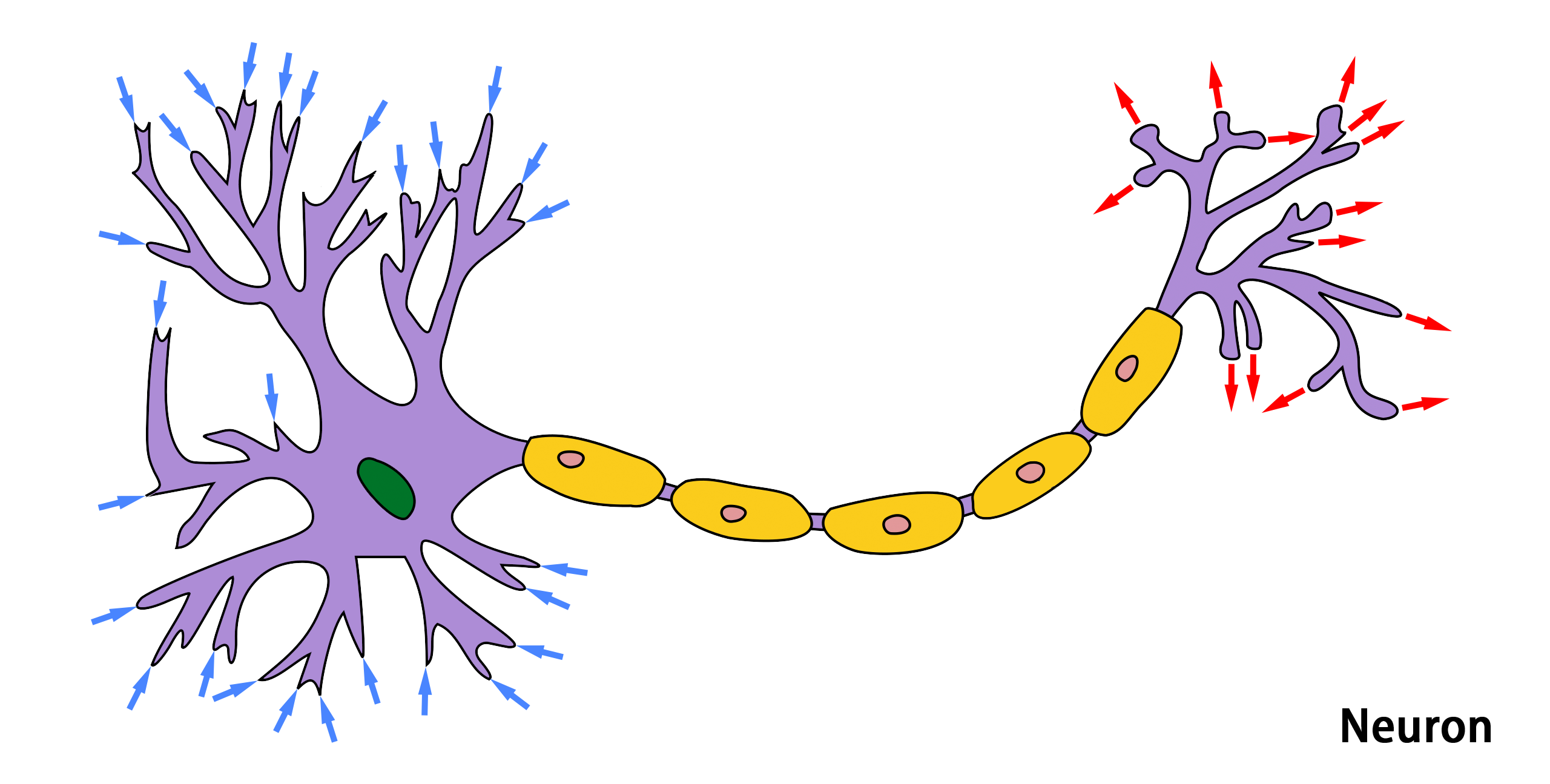
神經元 Neuron

Definition

\begin{align}
& \vec{\textbf{X}} & := & \text{ Input} \\
& \hat{\textbf{Y}} & := & \text{ Output} \\
& & = & \ f(\vec{\textbf{X}}) = g^{[i]}(\vec{\textbf{W}}^{[i]} \cdot \vec{\textbf{A}}^{[m – 1]} + \vec{\textbf{B}}^{[i]}) \\
& m & := & \text{ Number of layers} \\
\\
& \vec{\textbf{A}}^{[i]} & := & \text{ Activations from } i^{\text{th}} \text{ layer} \\
& & = & \ (\textit{a}^{[i]}_{1}, \textit{a}^{[i]}_{2}, …, \textit{a}^{[i]}_{j}) \\
& \vec{\textbf{A}}^{[1]} & = & g^{[1]}(\vec{\textbf{W}}^{[1]} \cdot \vec{\textbf{X}} + \vec{\textbf{B}}^{[1]}) \\
& \textit{a}^{[i]}_{j} & := & \text{ Activation from } j^{\text{th}} \text{ neuron in } i^{\text{th}} \text{ layer} \\
\\
& \vec{\textbf{W}}^{[i]} & := & \text{ Weights of } i^{\text{th}} \text{ layer} \\
& & = & \ (\vec{\textbf{w}}^{[i]}_{1}, \vec{\textbf{w}}^{[i]}_{2}, …, \vec{\textbf{w}}^{[i]}_{j}) \\
& \vec{\textbf{B}}^{[i]} & := & \text{ Biases of } i^{\text{th}} \text{ layer} \\
& & = & \ (\vec{\textbf{b}}^{[i]}_{1}, \vec{\textbf{b}}^{[i]}_{2}, …, \vec{\textbf{b}}^{[i]}_{j}) \\
& g^{[i]}(\vec{\textbf{W}}^{[i]}, \vec{\textbf{A}}^{[i]}, \vec{\textbf{B}}^{[i]}) & := & \text{ Transfer function of } i^{\text{th}} \text{ layer}
\end{align}

Layer i

$$ \vec{\textbf{A}}^{[i]} = g^{[i]}(\vec{\textbf{W}}^{[i]} \cdot \vec{\textbf{A}}^{[i – 1]} + \vec{\textbf{B}}^{[i]}) $$

Last Updated on 2024/12/09 by A1go