Machine Learning 機器學習
Performance Metrics
Confusion Matrix
| Predicted Condition | |||
| Positive (PP) | Negative (PN) | ||
| Actuall Condition |
Positive (P) | True Positive | False Negative (Type II error) |
| Negative (N) | False Positive (Type I Error) |
True Negative | |
Total Population = P + N
準確率 Accuracy = (TP + TN) / (TP + FP + FN + TN)
全部樣本中的預測正確率
精確率 Precision = TP / (TP + FP)
預測陽性的樣本 (PP) 中的預測正確率
FP 越小越好 ⇔ 降低誤判 False 為 True 的可能性
- 安全系統
召回率 Recall = TP / (TP + FN)
陽性的樣本 (P) 中的預測正確率
提升 Positive (P) 中的預測正確率 ⇔ 盡可能地找出所有 P
- 人臉辨識找通緝犯
F1-score = 2 / [(1 / Precision) + (1 / Recall) ]
F-score 能兼顧 Precision 和 Recall
$$ F \textit{-} score :=\frac{(1 + \beta^2) Precision \times Recall}{\beta^2 \cdot Precision + Recall} $$
令 β 為 0 ⇒ F1-score:
$$ \frac{2}{F_1 \textit{-} score} = \frac{1}{Precision} + \frac{1}{Recall} \Rightarrow F_1 \textit{-} score = \frac{2}{\frac{1}{Precision} + \frac{1}{Recall}} $$
Supervised Learning 監督式學習
Defined by its use of labeled datasets
to train algorithms that to classify data (Classification)
or predict outcomes accurately (Regression).
Features
\begin{align}
x_j & := j^{th} \text{ feature} \\
n & := \text{number of features} \\
\vec{x}^{(i)} & := \text{features of } i^{th} \text{ training example} \\
x_j^{(i)} & := \text{value of feature } j \text{ in } i^{th} \text{ training example}
\end{align}
Data Annotation/Labeling
Data annotation is the process of labeling individual elements of training data (whether text, images, audio, or video) to help machines understand what exactly is in it and what is important. Data annotation also plays a part in the larger quality control process of data collection, as well-annotated datasets become ground truth datasets: data that is held up as a gold standard and used to measure model performance and the quality of other datasets.
Features Scaling
\begin{align}
\mu_{x} &: \text{mean of }x \\
\sigma_{x} &: \text{standard deviation of }x
\end{align}
Mean Normalization
$$ x^{(i)} = \frac{x^{(i)} – \mu_{x}}{\mathop{max}(x) – \mathop{min}(x)} $$
Z-score Normalization
$$ x^{(i)} = \frac{x^{(i)} – \mu_{x}}{\mathop{\sigma_{x}}} $$
Feature Engineering
Using intuition to design new features,
by transforming or combining original features.
Regression Analysis 迴歸分析 (應變數 Y 為連續)
定義
尋找一至多個自變數 X / [X_1, X_2, …, X_n] 和應變數 Y 之間關係的 model f
\begin{align}
(x^{(i)} , y^{(i)}) \ 或 \ ([x_1^{(i)}, x_2^{(i)}, …, x_n^{(i)}], y^{(i)}) & := i^{th} \text{ training example} \\
\hat{y}^{(i)} = f(x^{(i)}) \ 或 \ \hat{y}^{(i)} = f(x_1^{(i)}, x_2^{(i)}, …, x_n^{(i)}) & := \text{model}
\end{align}
※ 自變數 (Independent Variable):
![]() 「因 (cause)」、features;用以解釋其他變數
「因 (cause)」、features;用以解釋其他變數
※ 應變數 (Dependent Variable):
![]() 「果 (effect)」、targets;被解釋的變數
「果 (effect)」、targets;被解釋的變數
Linear Regression 線性迴歸
- Univariate Linear Regression Model(單變數線性迴歸模型)
$$ \hat{y} = f_{w, b}(x) = w \dot x + b $$ - Multiple Linear Regression Model(單變數線性迴歸模型)
$$ \hat{y} = f_{\vec{w}, b}(\vec{x}) = w_1 \dot x_1 + w_2 \dot x_2 + … + w_n \dot x_n + b $$
Cost Function
A cost function J is an important parameter that determines how well a machine learning model performs for a given dataset. The goal is to find the values of model parameters for which the cost function return as small a number as possible.
$$ \text{Goal: Find } \mathop{min \ }_{\theta_1, \theta_2, …}{J(\theta_1, \theta_2, …)} $$
Squared Error Cost Function
\begin{align}
& J(\theta_1, \theta_2, …) = \frac{1}{2m}\sum_{i = 1}^{m}{(\hat{y}^{(i)} – y^{(i)})^2} \\
& \theta_1, \theta_2, … := \text{parameters of } y = f(x)
\end{align}
Polynomial Regression 多項式迴歸
$$ \hat{y} = f_{\vec{w}, b}(x) = w_1 \dot x + w_2 \dot x^2 + … + w_n \dot x^n + b $$
Gradient Descent
$$ \theta_{k + 1} = \theta_k – \alpha \frac{\partial}{\partial \theta} J $$
Gradient descent is a first-order iterative optimization algorithm for finding a local minimum of a differentiable function. The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point.
Checking Gradient Descent for Convergence.
\begin{eqnarray}
& \text{Convergence } : \text{ If } J_k – J_{k – 1} < \varepsilon & \\
& \varepsilon : \text{ A variable representing a small number (such as 0.001)} &
\end{eqnarray}
Choosing the learning rate.
- Make sure α > 0 with a proper size.
- You may start like by trying a learning rate of 0.001
and try learning rate as 10 times as large say 0.01 and 0.1 and so on.
Classification 分類(應變數 Y 為離散)
Predict categories.
Decision Boundary
In a statistical-classification problem with two classes,
a decision boundary or decision surface
is a hypersurface that partitions the underlying vector space into two sets,
one for each class.
The classifier will classify all the points on one side of the decision boundary
as belonging to one class
and all those on the other side as belonging to the other class.
Logistic Regression
Logistic regression is a binary classification method.
Sigmoid Function
$$ g(z) = \tfrac{1}{1 + e^{-z}} \quad 0 < g(z) < 1 $$
Logistic Function
$$ f(x) = \frac{L}{1 + e^{-k(x – x_0)}} $$
\begin{align}
& x_0 \text{: the } x \text{ value of the function’s midpoint} \\
& L \text{: the supremum of the values of the function} \\
& k \text{: the logistic growth rate or steepness of the curve}
\end{align}
Definition of Logistic Regression
\begin{align}
& \text{Let } z = 0 \text{ is the decision boundary.} \\
& P(Y = 1|X = x) = g(z) = \frac{1}{1 + e^{-z}} \text{ is the “probability” that y is 1.} \\
& \hat{y} =
\begin{cases}
1 &\quad \text{if } P(Y = 1|X = x) \geq \text{threshold (usually 0.5)} \\
0 &\quad \text{otherwise}
\end{cases}
\end{align}
Loss Function
Unlike the lost function used in linear regression is always a convex function,
\begin{align}
L(\hat{y}, y) =
\begin{cases}
-log(\hat{y}^{(i)}) &\quad \text{if } y^{(i)} = 1 \\
-log(1 – \hat{y}^{(i)}) &\quad \text{if } y^{(i)} = 0
\end{cases}
\end{align}
Simplified:
$$ L(\hat{y}, y) = -y^{(i)} log(\hat{y}^{(i)}) – (1 – y^{(i)})log(1 – \hat{y}^{(i)}) $$
Cost Function
$$ J = \frac{1}{m}\sum^m_{i = 1}L(\hat{y}^{(i)}, y^{(i)}) = -\frac{1}{m}\sum^m_{i = 1}(y^{(i)} log(\hat{y}^{(i)}) + (1 – y^{(i)})log(1 – \hat{y}^{(i)})) $$
Ensemble learning
In statistics and machine learning,
ensemble methods use multiple learning algorithms
to obtain better predictive performance
than could be obtained from any of the constituent learning algorithms alone.
Boosting
A strong learner created by a set of weak.
A weak learner is defined to be a classifier
that is only slightly correlated with the true classification.
(It can label examples better than random guessing)
In contrast,
a strong learner is a classifier
that is arbitrarily well-correlated with the true classification.
Random Forest
k-Nearest Neighbors Algorithm
Support Vector Machine
Relevance Vector Machine
Neural Network 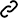
Underfitting | Generalization | Overfitting
Our goal when creating a model
is to be able to use the model to predict outcomes correctly for new examples.
A model which does this is said to generalize well.
Underfitting: High Bias
Underfitting occurs when a mathematical model
cannot adequately capture the underlying structure of the data.
An under-fitted model is a model where some parameters or terms
that would appear in a correctly specified model are missing.
Under-fitting would occur,
for example, when fitting a linear model to non-linear data.
Such a model will tend to have poor predictive performance.
泛化 Generalization: Just Right
Overfitting: High Variance
In mathematical modeling, overfitting is
“the production of an analysis that corresponds too closely or exactly to a particular set of data,
and may therefore fail to fit additional data or predict future observations reliably”.
An overfitted model is a mathematical model
that contains more parameters than can be justified by the data.
In a mathematical sense,
these parameters represent the degree of a polynomial.
The essence of overfitting is
to have unknowingly extracted some of the residual variation (i.e., the noise)
as if that variation represented the underlying model structure.
Addressing Overfitting
To Collect More Training Data
One way to address Overfitting is to collect more training data.
If you’re able to get more data, with the larger training set,
the learning algorithm will learn to fit a function that is less wiggly.
You can continue to fit a high-order polynomial
or some of the functions with a lot of features,
and if you have enough training examples, it will still do okay.
But getting more data isn’t always an option.
Feature Selection
If you have too many features but don’t have enough training data,
then your learning algorithm may also overfit to your training set.
If we were to pick just a subset of the most useful ones.
If you think those are the most relevant features,
then using just that smallest subset of features,
you may find that your model no longer overfits as badly.
One way you could do so is to use your intuition
to choose what you think is the best set of features.
Choosing the most appropriate set of features to use
is sometimes also called feature selection.
Now, one disadvantage of feature selection
is that by using only a subset of the features,
the algorithm is throwing away some of the information,
useful features could be lost.
Maybe you don’t want to throw away some of the information
by throwing away some of the features.
Regularization 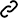
Regularization lets you keep all of your features,
but they just prevent the features from having an overly large effect,
which is what sometimes can cause overfitting.
Unsupervised Learning 非監督式學習
Clustering 分群
Dimensionality Reduction 降維
Anomaly Detection 異常檢測
Reinforcement learning 強化學習
Recommender system 推薦系統
Last Updated on 2023/08/02 by A1go

