Leetcode # 439. Ternary Expression Parser
- 2023.07.25
- ★★ Medium LeetCode Parsing
- TernaryConditionalOperator
https://leetcode.com/problems/ternary-expression-parser
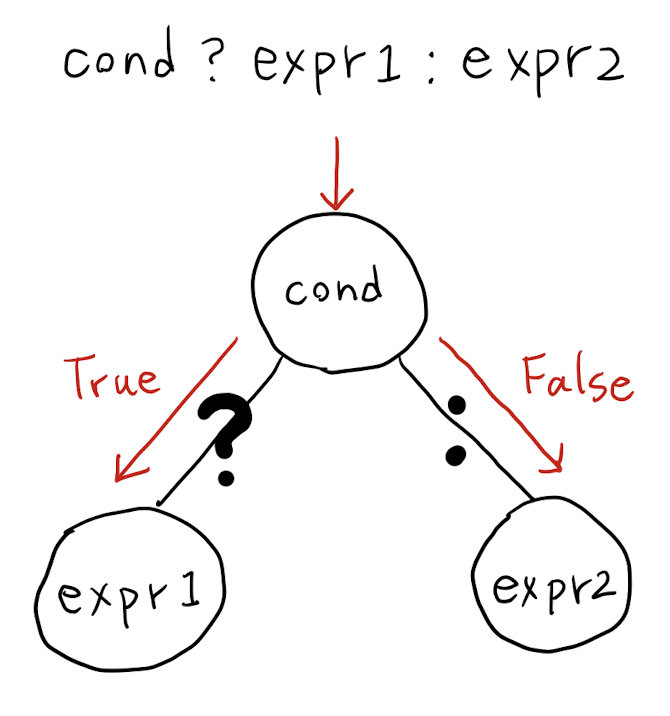
三元條件運算子 Ternary Conditional Operator
variable |
= | condition ? value_if_true : value_if_false |
or condition ? expr1 : expr2 |
Solution (Stack)
根據:
The conditional expressions group right-to-left (as usual in most languages).
「三元條件運算子」優先順序在大多數程式語言中為「由右至左」
故,Example 2 的 F ? 1 : T ? 4 : 5 ≡ F ? 1 : (T ? 4 : 5)
所以使用 stack 時,要將 expression 逆序存取 (for e in lst[::-1])
在先收集到「」後再收集到「」之後
下一個運算式 (expression ,指 condition ) 完結之時
依序取出 stack 中的「?」、「expr1」、「:」、「expr2」
再將三元條件運算子的結果存放回 stack 中
註:本解答未驗證 expression 為 valid 與否
Time Complexity: O(len(expression))
Space Complexity: O(len(expression))
(The input and output generally do not count towards the space complexity.)
class Solution:
def parseTernary(self, expression: str) -> str:
stack = []
for c in expression[::-1]:
if stack and stack[-1] == "?":
stack.pop()
expr1 = stack.pop()
stack.pop()
expr2 = stack.pop()
stack.append(expr1 if c == "T" else expr2)
else:
stack.append(c)
return stack[0]
Solution (Binary Tree)
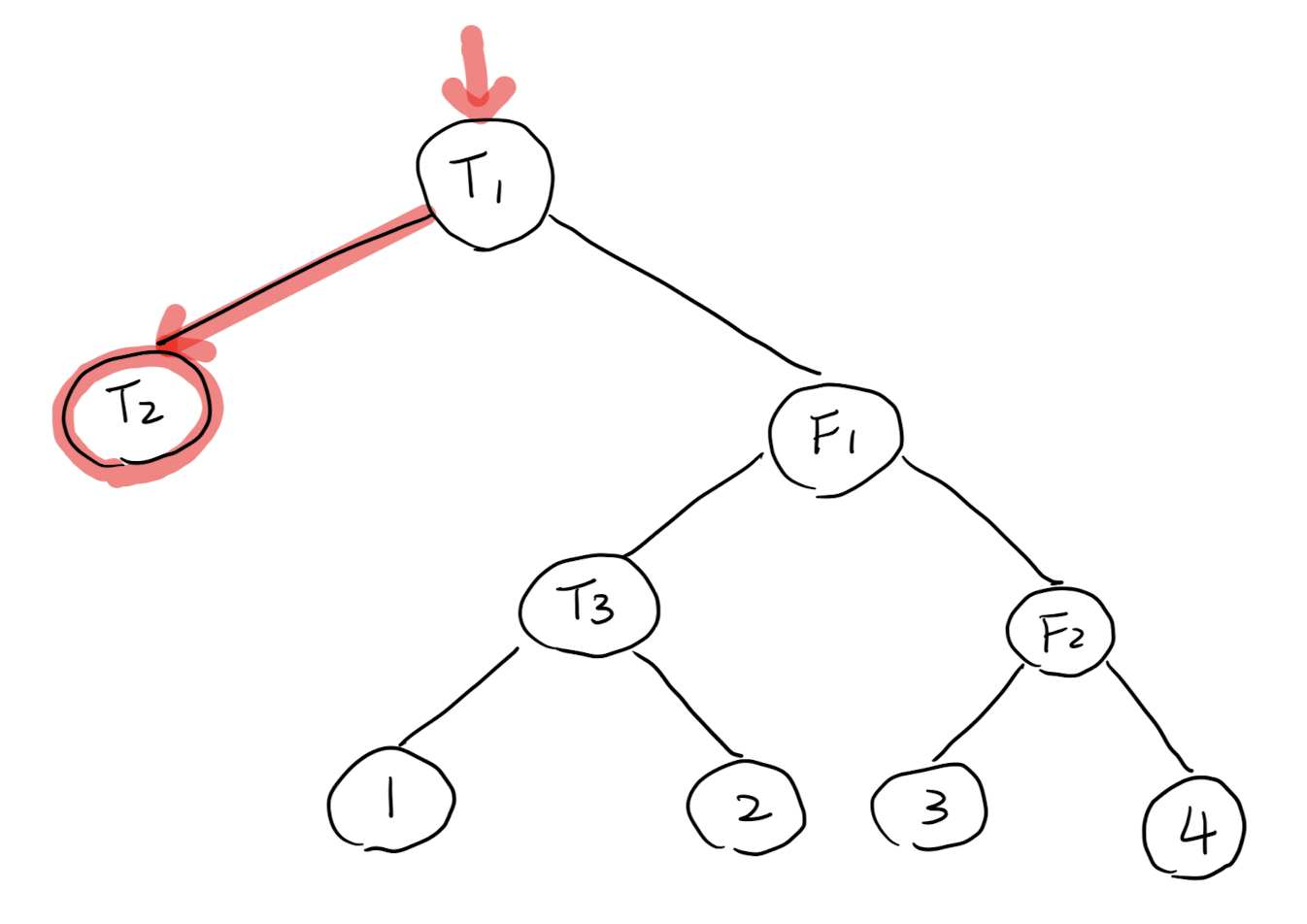
例:
T1 ? T2 : F1 ? T3 ? 1 : 2 : F2 ? 3 : 4
= T1 ? T2 : [F1 ? (T3 ? 1 : 2) : (F2 ? 3 : 4)]
Time Complexity: O(len(expression))
Space Complexity: O(len(expression))
(The input and output generally do not count towards the space complexity.)
class Solution:
def parseTernary(self, expression: str) -> str:
self.i = 0
def construct_tree():
root = TreeNode(expression[self.i])
self.i += 1
if self.i == len(expression): return root
if expression[self.i] == "?":
self.i += 1
root.left = construct_tree()
self.i += 1
root.right = construct_tree()
return root
cur = construct_tree()
while cur.left and cur.right:
cur = cur.left if cur.val == "T" else cur.right
return cur.val
Constant Space Solution
只使用 O(1) 的空間
- 如果
cond為T
走到這一層的expr1(i += 2) - 如果
cond為F
利用count走到這一層的expr2 - 是否有下一層的 Ternary Conditional Operator ?
- 如果下一個
char不是T或F
則為expr1或expr2其中之一
即沒有下一層的cond,回傳 - 如果下一個
char是T或F:- 是最後一個
char
⇒ 亦為最後一個expr2,回傳 - 再下一個
char是:- 下一個
:屬於現在的 Ternary Conditional Operator
則前一個字元為?
意即現在這個字元位於?和:之間 ⇒ 為本層的expr1,回傳 - 下一個 : 屬於另一個 Ternary Conditional Operator
前一個 : 屬於現在的 Ternary Conditional Operator
意即現在這個字元位於兩個:之間 ⇒ 為本層的expr2,回傳
- 下一個
- 如果都不符合 3 – 1、3 – 2 – 1、3 – 2 – 2
則為cond回到 1.
- 是最後一個
- 如果下一個
Time Complexity: O(len(expression))
Space Complexity: O(1)
(The input and output generally do not count towards the space complexity.)
class Solution:
def parseTernary(self, expression: str) -> str:
i = 0
while True:
# Early Return
# Condition 1 of if statement here:
# expression[i] not in "TF"
# ↪︎ Means it's not a "cond".
# Condition 2 of if statement here:
# i == len(expression) - 1
# ↪︎ Means it's final "expr2".
# Condition 3 of if statement here:
# expression[i + 1] == ":"
# ↪︎ This ":" belongs another Ternary Conditional Operator,
# and the previous ":" belongs this Ternary Conditional Operator,
# so expression[i] is "expr2" of this Ternary Conditional Operator.
if expression[i] not in "TF" \
or i == len(expression) - 1 \
or expression[i + 1] == ":":
return expression[i]
#------------------------------
# Reduced from:
# if expression[i] == "T":
# i = i + 2
# else:
# i = i + 2
i = i + 2
if expression[i - 2] != "T":
#------------------------------
# ↓
# T ? (expr1) : (expr2)
# ↓
# F ? (expr1) : (expr2)
count = 1
while count != 0:
if expression[i] in "?:":
count += 1 if expression[i] == "?" else -1
i += 1
Last Updated on 2023/08/16 by A1go

