Leetcode # 1183. Maximum Number of Ones
- 2023.08.29
- ★★★ Hard Greedy Method LeetCode
Problem
https://leetcode.com/problems/max-consecutive-ones-iii
Solution: Greedy Method
k := sideLength
當 square 橫向移動
grid[i:i + k, j].count(1) == grid[i:i + k, j + k].count(1)
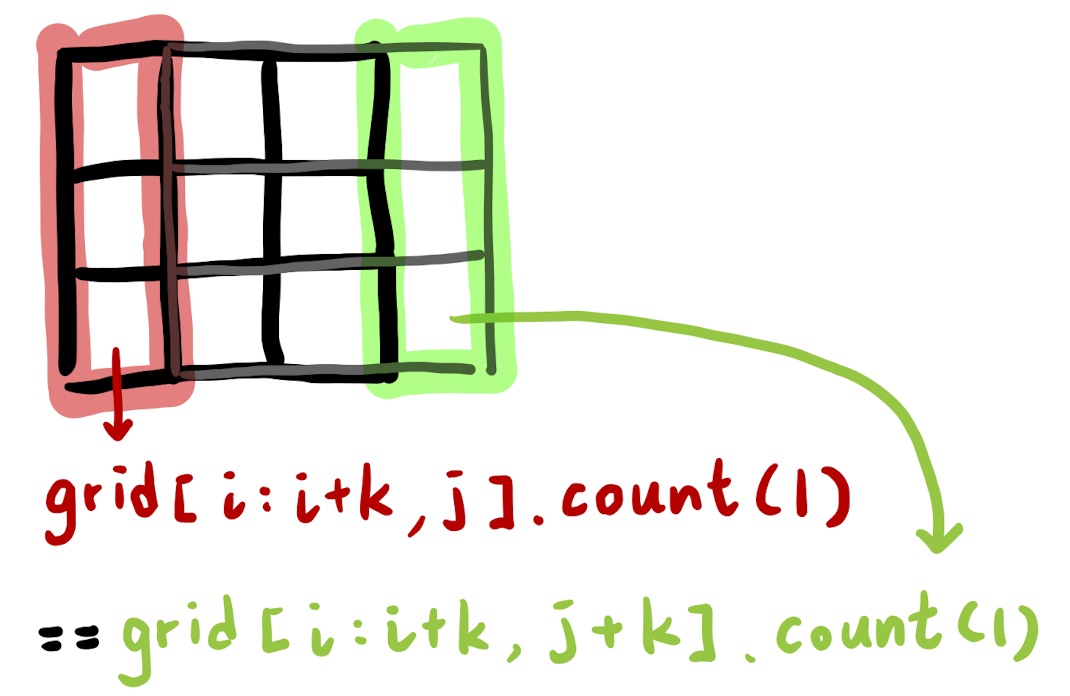
同理,縱向移動時,
grid[i, j:j + k].count(1) == grid[i + k, j:j + k].count(1) 亦會成立
⇒ 令 grid[i + a * k][j + b * k] = grid[i][j] 就能使上述兩點成立
(i + a * k < width; j + b * k < width; a, b = 0, 1, 2, …)
| square[i][j] | := | |
| = | ((height – 1 – i) // k + 1) * ((width – 1 – j) // k + 1) |
回傳前 maxOnes 大的 square[i][j] 之總和即可
Time Complexity: O(w * h * (k ** 2) + (k * log(k)) ** 2) = O((k * log(k)) ** 2)
![]() w := width, h := height
w := width, h := height
![]() 計算 square 使用的 time complexity: O(
計算 square 使用的 time complexity: O(w * h * (k ** 2))
![]() 排序 square 使用的 time complexity: O((k * log(k)) ** 2)
排序 square 使用的 time complexity: O((k * log(k)) ** 2)
Space Complexity: O(k ** 2)
(The input and output generally do not count towards the space complexity.)
class Solution:
def maximumNumberOfOnes(self, width: int, height: int, sideLength: int, maxOnes: int) -> int:
square = [[len([None for x in range(i, height, sideLength) for y in range(j, width, sideLength)]) \
for j in range(sideLength)] \
for i in range(sideLength)]
return sum(sorted([square[i][j] for i in range(sideLength) for j in range(sideLength)], reverse = True)[:maxOnes])
Mathmatical Solution
nw := w // k, nh :=h // k
rw := w % k, rh := h % k
square := 有maxOnes個1其餘為0的 k * k 方形
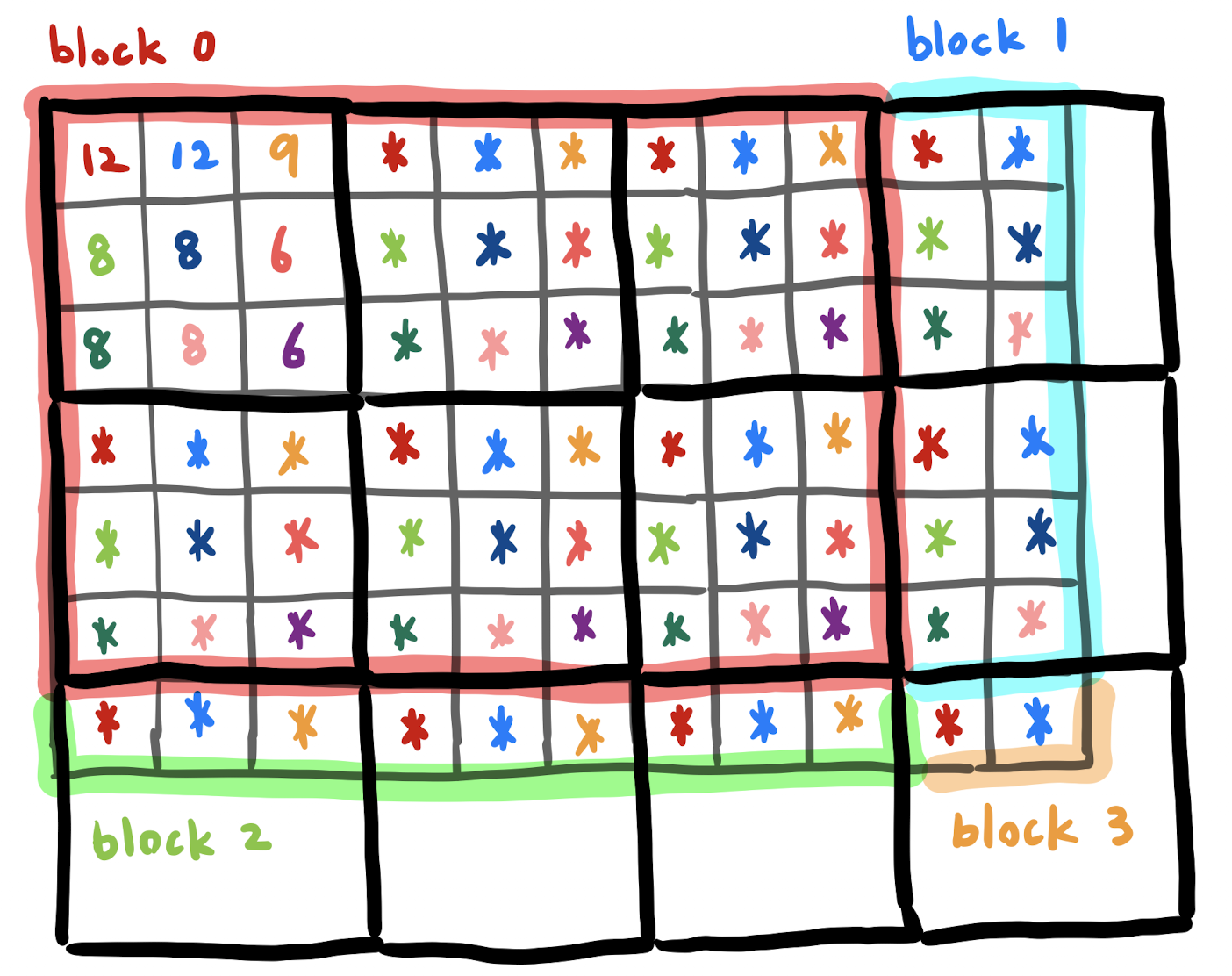
如圖所示,將 grid 分成四個 block

| block 1: |
有 |
| block 2: |
有 |
| block 3: |
有 |
| block 4: |
|
- 其中 block 4 的
square[:rh, :rw]
被包含於 block 2 的square[:, :rw]和 block 3 的square[:rh, :]之中
⇒ 分配rw * rh個1給square[:rh, :rw] - block 2 還沒被配置的
square[rh:, :rw]
以及 block 3 還沒被配置的square[:rh, rw:]
依照 nh 和 nw 的大小決定優先填滿 block 2 或 block 3 如果 block 2 和 block 3 都被填滿
再把剩下的1拿來填滿square[rh:, rw:]
Time Complexity: O(1)
Space Complexity: O(1)
(The input and output generally do not count towards the space complexity.)
class Solution:
def maximumNumberOfOnes(self, width: int, height: int, sideLength: int, maxOnes: int) -> int:
nw, nh = width // sideLength, height // sideLength
rw, rh = width % sideLength, height % sideLength
ones_in_block3 = min(maxOnes, (rh) * (rw))
remained_ones = maxOnes - ones_in_block3
block1_size = rw * (sideLength - rh)
block2_size = (sideLength - rw) * rh
if nh > nw:
ones_in_block1 = min(remained_ones, block1_size)
ones_in_block2 = min(remained_ones - ones_in_block1, block2_size)
else:
ones_in_block2 = min(remained_ones, block2_size)
ones_in_block1 = min(remained_ones - ones_in_block2, block1_size)
# print(f"{nh} * [{sideLength} × {rw}] ({ones_in_block1}), {nw} * [{rh} × {sideLength}] ({ones_in_block2})")
ones = (nw) * (nh) * maxOnes
ones += (nh) * (ones_in_block1 + ones_in_block3)
ones += (nw) * (ones_in_block2 + ones_in_block3)
ones += ones_in_block3
return ones
Last Updated on 2023/08/29 by A1go

