Binary Tree 二元樹
定義
binary tree 的每一個 node 最多只有兩個 subnode (子節點)
Complete Binary Tree(完全二元樹)
- 最後一層以外的層全部都是滿的
- 最後一層的節點全部向左靠
Binary Search Tree
\begin{align}
& \forall \text{ internal node } n \text{:} \\
& \text{1. } \forall l \in (n \text{‘s left subtree}), n \text{.key} > l \text{.key} \\
& \text{2. } \forall r \in (n \text{‘s right subtree}), n \text{.key} < r \text{.key}
\end{align}
Template of Searching
curr = root
while ...condition_about_curr...:
curr = curr.right if {curr.val is too small} else curr.left
return curr
相關例題
- Leetcode # 235. Lowest Common Ancestor of a Binary Search Tree
- Leetcode # 270. Closest Binary Search Tree Value
- Leetcode # 701. Insert into a Binary Search Tree
相關文章
Traversal 遍歷
總覽
| 方法 | Complexity |
| 深度優先搜尋(Depth-First Search; use stack) 廣度優先搜尋(Breadth-First Search; use queue) |
Time Complexity: O(N) Space Complexity: O(N) |
| Recursive | Time Complexity: O(N) Space Complexity: O(N) |
| Morris Traversal | Time Complexity: O(N) Space Complexity: O(1) |
DFS
stack = [root]
while stack:
cur = stack:pop()
if cur is leaf:
...do some operation ...
if cur.left:
stack.attend(cur.left)
if cur.right:
stack.attend(cur.right)
BFS (Level Order Traversal)
queue = collections.deque(root)
while queue:
cur = queue.popleft()
if cur is leaf:
...do some operation ...
if cur.left:
queue.attend(cur.left)
if cur.right:
queue.attend(cur.right)
前序/中序/後序 (Preorder / Inorder / Postorder) Traversal
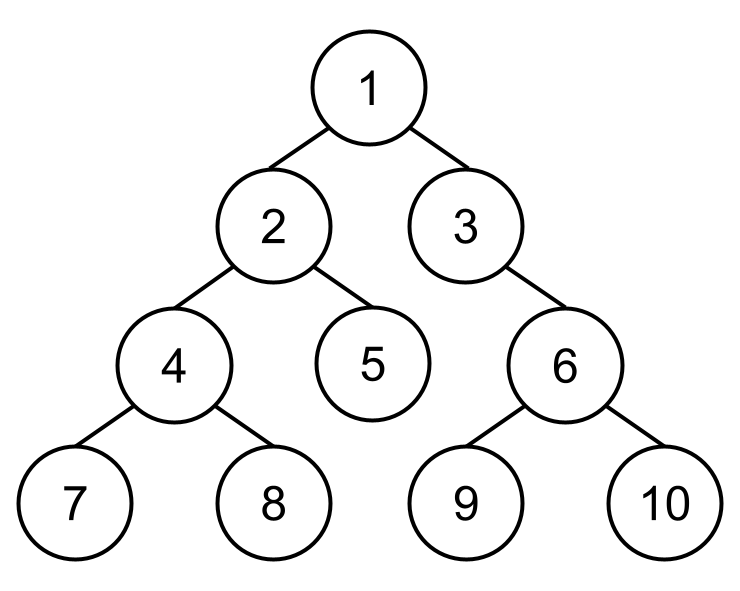
- 前序:根節點 → 左子樹 → 右子樹
(1 2 4 7 8 5 3 6 9 10) - 中序:左子樹 → 根節點 → 右子樹
(7 4 8 2 5 1 3 9 6 10) - 後序:左子樹 → 右子樹 → 根節點
(7 8 4 5 2 9 10 6 3 1)
Predecessor/Successor (上一個/下一個 node)
- Predecessor: 上一個 node
- Successor: 下一個 node
Pre-order/In-order/Post-order Traversal in Recursive
def traversal(root, order):
if root is None:
return []
if order = "pre":
return [cur] + traversal(cur.left) + traversal(cur.right)
if order = "in":
return traversal(cur.left) + [cur] + traversal(cur.right)
if order = "post
return traversal(cur.left) + traversal(cur.right) + [cur]
Expression Tree
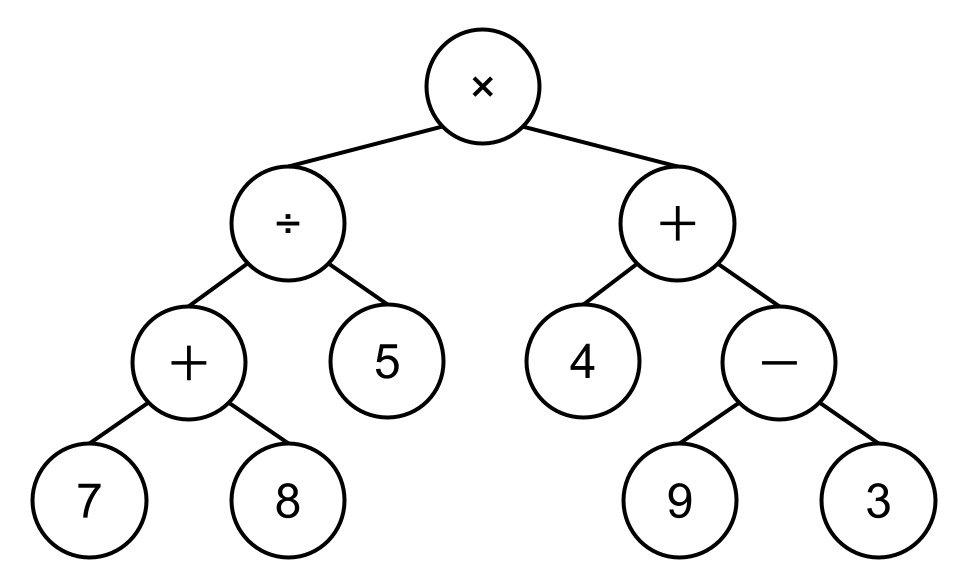
- 前序 (Prefix) 或 波蘭表示法 (Polish notation)
[× ÷ + 7 8 5 + 4 – 9 3] - 中序 (Infix) :一般習慣的四則運算表示法
[((7 + 8) ÷ 5) × (4 + 9 – 3)] - 後序 (Postfix) 或 逆波蘭表示法 (Reverse Polish notation)
[7 8 + 5 ÷ 4 9 3 – + ×]
Threaded Binary Tree
將未使用的 left/right subtree pointer
作為指向此 node 的 in-order predecessor/successor 的thread
Morris Traversal
和 Threaded Binary Tree 相同
使用未使用的 left/right subtree pointer
在移動前,先將現在位置 current
借用 predecessor.right 來記錄 (step 2.1)
這是我們第一次來到這個節點,之後向左移動
將來走到這個被修改過的 predecessor 後
利用現在的紀錄移動至 current 即當下的 seccessor 後 (step 1.)
再將該 predecessor.right 回復為空 (step 2.2)
這是我們再次回到這個節點,
並且已經遍歷完成左子樹,之後向左移動
Morris Traversal 的優點是
space complexity 為 O(1)
並且最終會將樹恢復為原狀
In-order Traversal
中序:左子樹 → 根節點 → 右子樹
輸出 current 的條件
- 沒有左子樹
- predecessor.right 不為空
⇒ 表示我們已遍歷完左子樹
流程
- 如果 current.left 為空,則輸出 current,
且將 current 設為 current.right - 如果 current.left 不為空,
則找到 current 的 predecessor (左子樹的 most right node )- 如果 predecessor.right 為空,
則將 predecessor.right 設為 current ,
將 current 設為 current.left - 如果 predecessor.right 不為空,
則將 predecessor.right 設為空(將樹恢復原狀)。
輸出 current ,將 current 設為 current.right
- 如果 predecessor.right 為空,
- 直到 current 為空停止
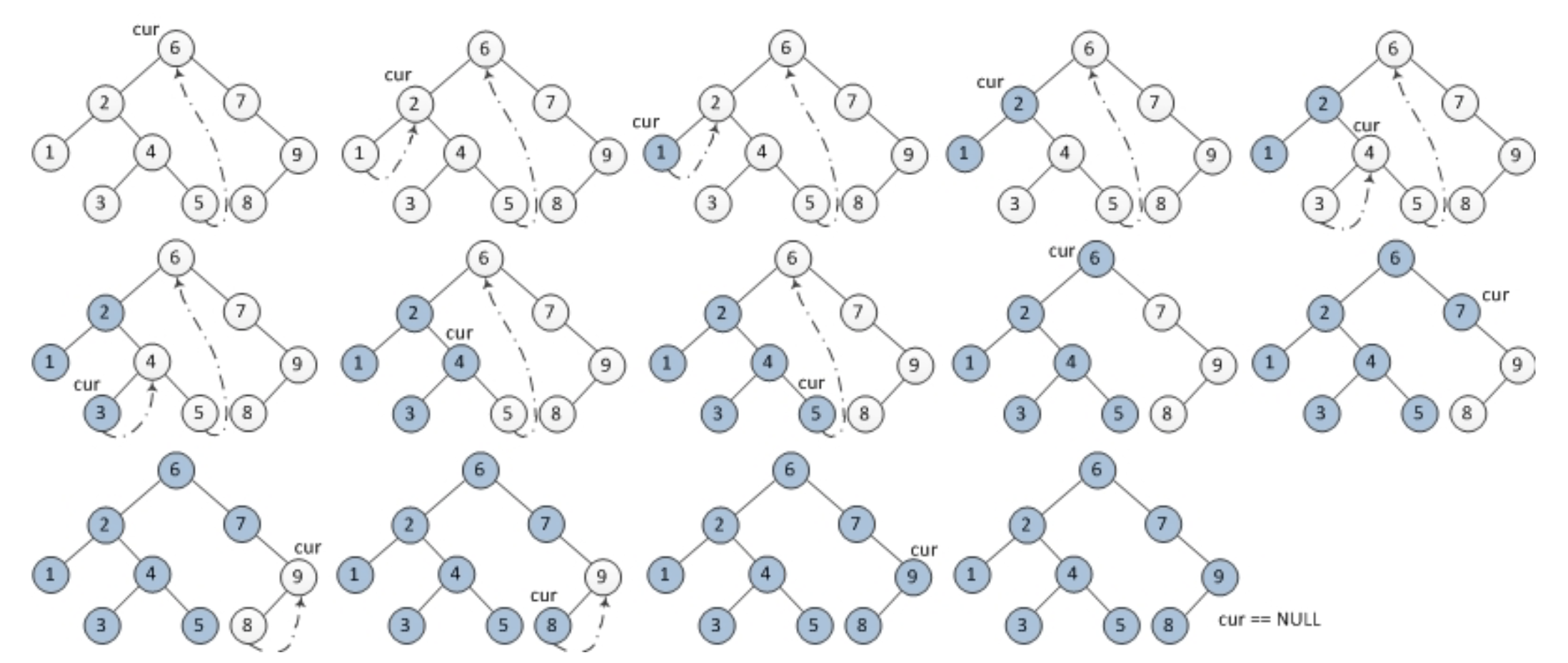
LeetCode # 94. Binary Tree Inorder Traversal
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if not root: return []
return (self.inorderTraversal(root.left) if root.left else []) \
+ [root.val] \
+ (self.inorderTraversal(root.right) if root.right else [])
Pre-order Traversal
前序:根節點 → 左子樹 → 右子樹
輸出 current 的條件
- 沒有左子樹
- 去左子樹之前
也就是我們尚未變更 predecessor.right
predecessor.right 尚為空的時候
流程
- 如果 current.left 為空,則輸出 current,
且將 current 設為 current.right - 如果 current.left 不為空,
則找到 current 的 predecessor (左子樹的 most right node )- 如果 predecessor.right 為空,輸出 current
並將 predecessor.right 設為 current ,
將 current 設為 current.left - 如果 predecessor.right 不為空,
則將 predecessor.right 設為空(將樹恢復原狀)。
將 current 設為 current.right
- 如果 predecessor.right 為空,輸出 current
- 直到 current 為空停止
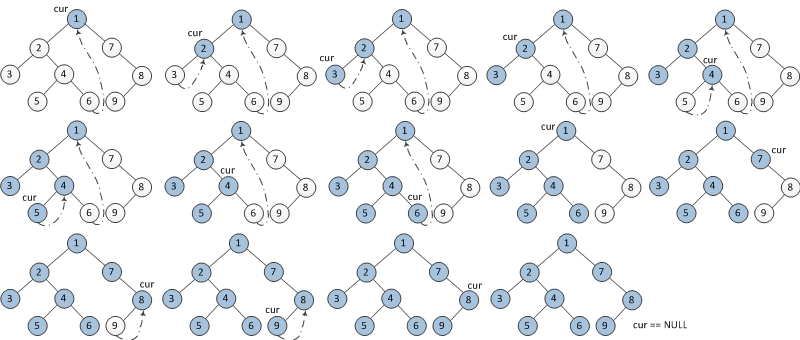
Post-order Traversal
後序:左子樹 → 右子樹 → 根節點
流程
前置作業:
令 dump = Node(0, root, 空)
current = dump
- 如果 current.left 為空,
將 current 設為 current.right - 如果 current.left 不為空,
則找到 current 的 predecessor (左子樹的 most right node )- 如果 predecessor.right 為空
並將 predecessor.right 設為 current ,
將 current 設為 current.left - 如果 predecessor.right 不為空,
則將 predecessor.right 設為空(將樹恢復原狀)。
從 predecessor 輸出至 current.left (from current.left to predecessor 的逆向輸出),
將 current 設為 current.right
- 如果 predecessor.right 為空
- 直到 current 為空停止
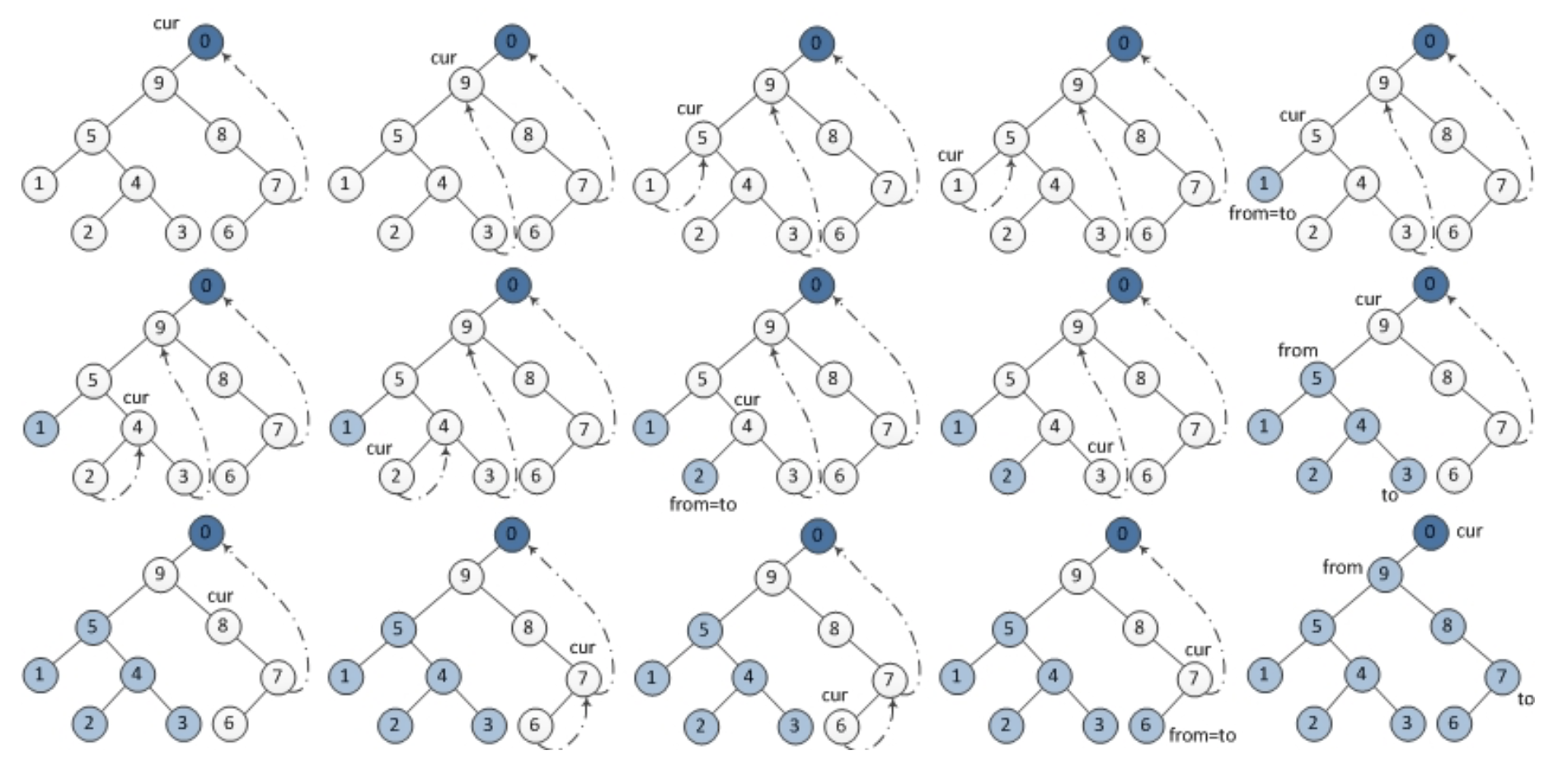
逆向輸出
# Reverse the tree nodes 'from' -> 'to'.
# You should can arrive 'to' from 'from'
# by each passed node's right subtree pointer.
def reverse(_from, to):
if _from == to: return
x, y = _from, _from.right
while True:
y, y.right, x = y.right, x, y
if x == to: break
# Print the reversed tree nodes 'from' -> 'to'.
def print_reverse(_from, to):
reverse(_from, to);
p = to
while True:
print(p.val)
if p == _from: break
p = p->right
reverse(to, _from)
相關例題
Others
Definition for a Binary Tree Node in LeetCode
Python
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
[Python] Binary Tree to List
def binary_tree_to_list(root, level=0):
if root is None:
return []
btree_in_list = []
curr_level = [root]
has_next_level = True
while has_next_level:
has_next_level = False
next_level = []
val_this_level = []
for node in curr_level:
if node:
has_next_level = True
next_level += [node.left, node.right]
val_this_level.append(node.val)
else:
next_level += [None] * 2
val_this_level.append(None)
btree_in_list += val_this_level if has_next_level else []
curr_level = next_level
for i in range(len(btree_in_list) - 1, -1, -1):
if btree_in_list[i]:
return btree_in_list[:i + 1]
Last Updated on 2024/04/27 by A1go

