Leetcode # 2779. ⭐️ Maximum Beauty of an Array After Applying Operation

Problem

https://leetcode.com/problems/maximum-beauty-of-an-array-after-applying-operation

Solution

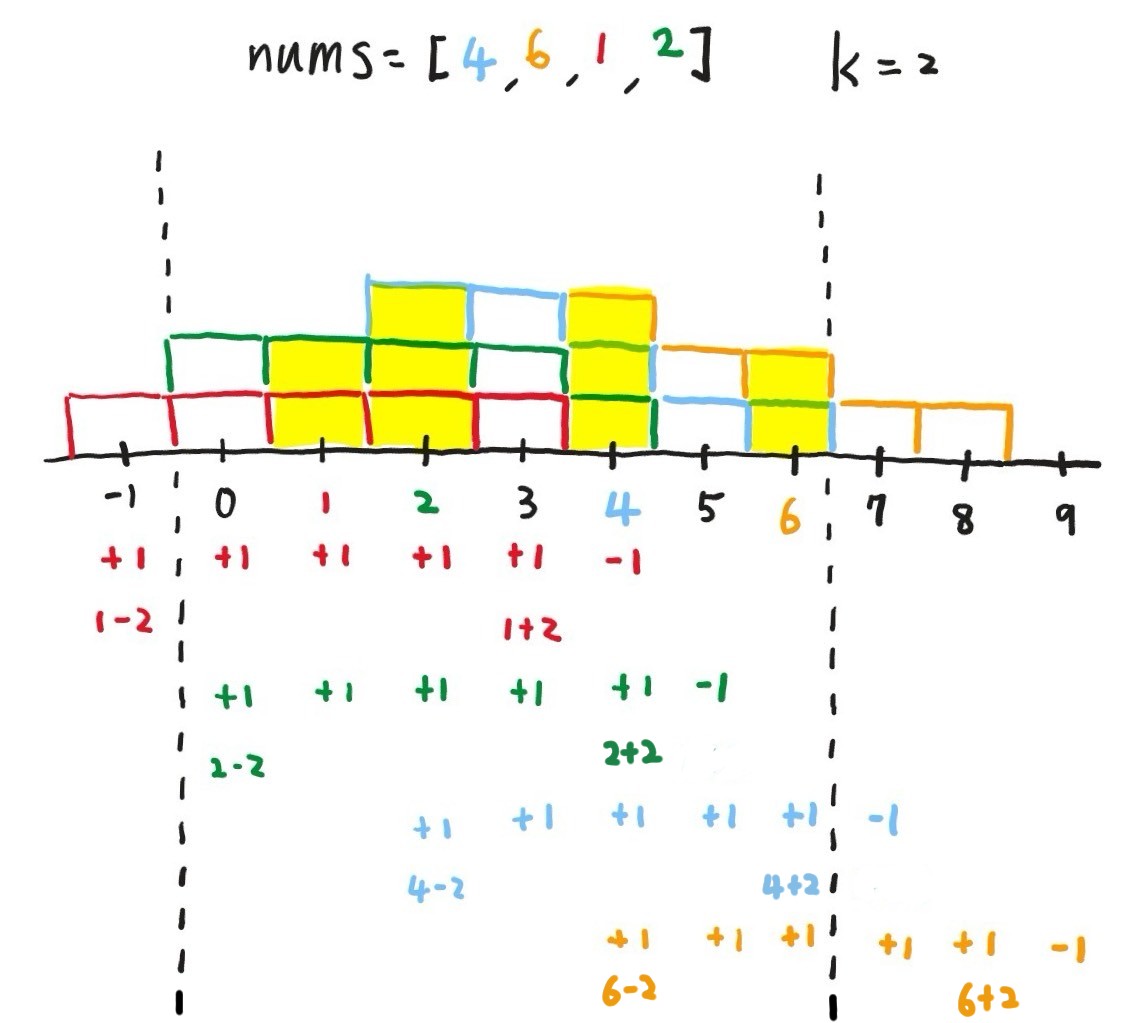
n ∈ nums, you can replace it with any integer from the range [n – k, n + k]
⇒ plus 1 (+1) from (n – k) to (n + k), and minus it (-1) at (n + k + 1)

Time Complexity: O(len(nums) + max(nums))
Space Complexity: O(max(nums))
(The input and output generally do not count towards the space complexity.)

class Solution:
  def maximumBeauty(self, nums: List[int], k: int) -> int:
    if len(nums) == 1: return 1

    ranges = Counter()
    max_n, min_n = 0, float("inf")
    for n in nums:
      ranges[n - k] += 1
      ranges[n + k + 1] -= 1
      max_n = max(max_n, n + k)
      min_n = min(min_n, n - k)
    
    cur = maximum = 0
    for n in range(min_n, max_n + 1):
      if n not in ranges: continue
      
      cur += ranges[n]
      maximum = max(maximum, cur)
    
    return maximum

Because the beauty of the array is
the length of the longest subsequence consisting of equal elements.
⇒ beauty of the array := [n] * len(nums), n ∈ nums
And ∀ n ∈ nums, n >= 0, so the boundary is [0, max(nums)]

class Solution:
  def maximumBeauty(self, nums: List[int], k: int) -> int:
    if len(nums) == 1: return 1

    ranges = Counter()
    max_n = max(nums)
    for n in nums:
      ranges[max(n - k, 0)] += 1
      ranges[min(n + k + 1, max_n)] -= 1
    
    cur = maximum = 0
    for n in range(max_n + 1):
      if n not in ranges: continue
      
      cur += ranges[n]
      maximum = max(maximum, cur)
    
    return maximum

Last Updated on 2024/12/12 by A1go