Pramp – BST Successor Search

Question

In a Binary Search Tree (BST), an Inorder Successor of a node is defined as the node with the smallest key greater than the key of the input node (see examples below). Given a node inputNode in a BST, you’re asked to write a function findInOrderSuccessor that returns the Inorder Successor of inputNode. If inputNode has no Inorder Successor, return null.

Explain your solution and analyze its time and space complexities.

Example

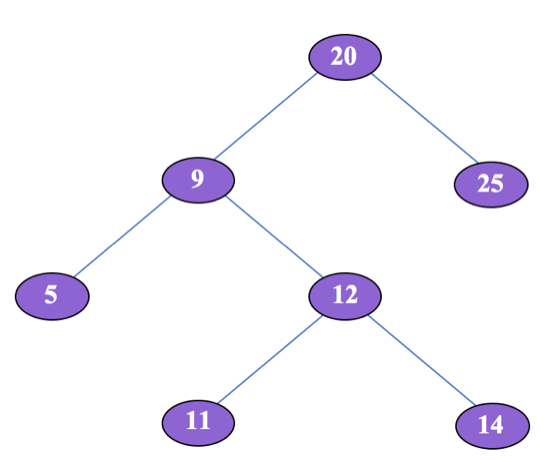
1. inputNode = 9, then Successor = 11
2. inputNode = 14, then Successor = 20
3. inputNode = 30, then Successor = None

Constraints

• [time limit] 5000ms
• [input] node
• [output] node

Solutions

1. 如果 inputNode 有 right child
   ⇒ 一直往左走，直到：
   1. right child rc.right = None ⇒ 回傳 rc
   2. right child rc.right < inputNode.key ⇒ 回傳 rc
2. 如果 inputNode 沒有 rightchild
   ⇒ 一直往上走，直到：
   1. 沒有更多 parent
   2. 某個 parent p.key > inputNode.key ⇒ 回傳 p

Time Complexity: O(size of)
Space Complexity: O(1)

def find_in_order_successor(self, inputNode):
  # inputNode has no right child
  if inputNode.right is None:
    cur = inputNode
    # Keep going to parent
    while cur:
      cur = cur.parent
      # While find some parent bigger than inputNode
      if cur.key > inputNode.key:
        return cur
    # No more parent can be found
    return None
  # inputNode has right child
  else:
    cur = inputNode.right
    while cur:
      # Keep going left 
      #   until no more left child
      #   or next left child is smaller than inputNode
      if cur.left is None or cur.left.key < inputNode.key:
        return cur
      cur = cur.left

Last Updated on 2023/08/16 by A1go